Modèle hydrogéologique

En hydrogéologie, la modélisation numérique s’applique à retranscrire, à l’aide de la programmation informatique, l’écoulement des eaux souterraines et la migration des polluants dans le système aquifère . La démarche de représentation théorique simplifiée d’un tel système comporte : la définition d’une structure (architecture ou géométrie des réservoirs), la formulation de lois (relations déterministes ou probabilistes) reliant les impulsions ou entrées du système à ses réponses ou sorties, la définition des paramètres (constants ou variables) entrant dans ces relations [Castany et Margat (1977) - Dictionnaire français d’hydrogéologie. BRGM , 249 p].

Objectifs des modèles numériques

Les modèles numériques sont utilisés en tant que :

• outil de compréhension, parce qu’ils permettent d’inventorier l’ensemble des données disponibles sur un site d’étude et de comprendre son fonctionnement. A contrario, ils identifient les zones en déficit d’informations, qui pourront être investiguées et les zones à surveiller ;
• outil de gestion et de prédiction des ressources et/ou de la qualité des eaux. Les modèles servent à prédire l’influence d’un pompage, estimer l’impact d’aménagements (barrage, bâtiments…) sur les niveaux d’eau dans les nappes et les débits dans les cours d’eau, prévoir l’évolution d’une pollution (trajectoires, temps de transfert, concentration), aider à la définition de schéma de gestion et/ou évaluer les conséquences des changements climatiques sur les réserves en eau.

Les modèles intègrent diverses équations mathématiques qui sont communément résolues au moyen de deux méthodes [Konikow L.F. (1996) - Numerical models of groundwater flow and transport. In : Manual on Mathematical Models in Isotope Hydrogeology, International Atomic Energy Agency Rept. IAEA-TECDOC-910, Vienna, Austria : 59-112] ; préalablement, le système aquifère doit être discrétisé (ou segmenté) en mailles (ou cellules) de formes variables :

• la méthode des différences finies consiste en des cellules parallélépipédiques rectangulaires, généralement cubiques, mais des modifications permettent de resserrer le maillage au niveau d’une zone d’intérêt, comme ici au droit du champ captant (b sur l'image),
• la méthode des éléments finis est représentée par des cellules polygonales quelconques (triangles, quadrilatères…) et offre donc plus de flexibilité dans la représentation d’un système irrégulier (c sur l'image).

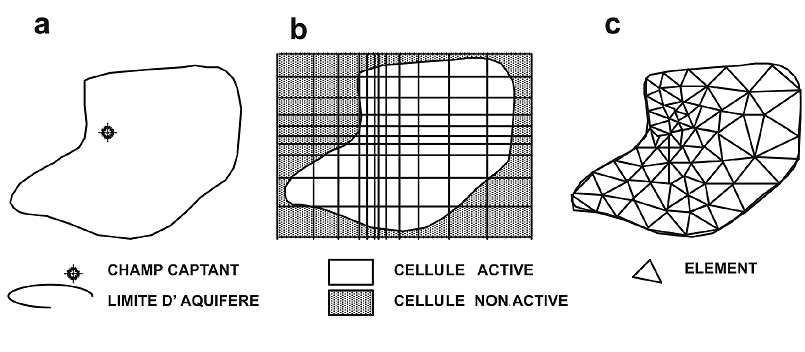
Discrétisation d’un aquifère à l’aide d’un maillage en différences finies -b- et en éléments finis -c-

Konikow L.F. (1996) - Numerical models of groundwater flow and transport. In : Manual on Mathematical Models in Isotope Hydrogeology, International Atomic Energy Agency Rept. IAEA-TECDOC-910, Vienna, Austria : 59-112

Même si chaque approche a des avantages et des inconvénients, il y a très peu de problèmes hydrogéologiques pour lesquels l’une est clairement meilleure que l’autre [Mook W.G. (2001) - Isotopes de l’environnement dans le cycle hydrologique. Chap.4 : Utilisation de modèles numériques pour simuler les processus d’écoulement et de transport dans les eaux souterraines : 174-215]. Les méthodes se différencient notamment par les difficultés de programmation et les précisions numériques.

Exemple de modélisation d’un aquifère en deux dimensions

On souhaite simuler l’écoulement de l’eau dans un aquifère , en deux dimensions, constitué d’une formation sableuse et d’une autre sablo-argileuse, avec une épaisseur constante. Il est bordé d’un plan d’eau au nord-ouest et d’une rivière à l’est. L’objectif est de retranscrire les hauteurs d’eau ainsi que les directions d’écoulement en chaque point de l' aquifère .

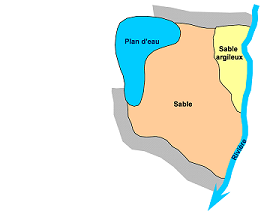
Représentation schématique d’un aquifère en deux dimensions

BRGM

La méthode choisie est celle des différences finies. Le maillage retenu est donc rectangulaire et régulier (figure ci-dessous). Le nombre, et donc la taille des mailles, est défini selon la précision des résultats souhaitée, des contours du système à modéliser ou encore de la puissance de l’ordinateur (plus il y a de mailles et plus les temps de calculs seront longs).
Au sein de chaque maille, sont renseignées les propriétés hydrauliques de l’ aquifère , comme sa perméabilité . Quand cela est possible, des valeurs d’infiltration (pluies efficaces) sont intégrées, parce qu’elles permettent de prendre en compte la recharge du système. Enfin, on renseigne les mailles où les niveaux piézométriques sont connus.

Dans notre exemple, on considère que l’altitude du plan d’eau est à un niveau piézométrique (H) constant. Cette charge est dite imposée (elle n’est pas calculée par la suite et sert de référence). De la même façon, on simule la rivière dont on connaît le niveau en amont et en aval. On applique une diminution linéaire entre ces deux points afin de renseigner la valeur du niveau de la rivière sur toutes les mailles recoupant son tracé.

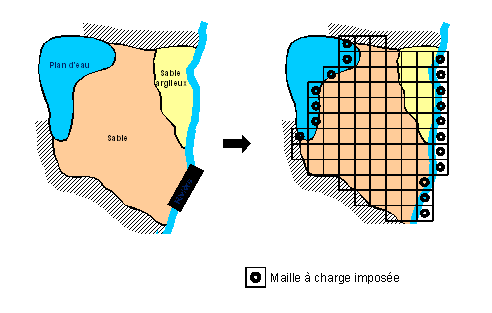
Création d’un maillage rectangulaire régulier représentant l’ aquifère

BRGM

Le modèle va maintenant résoudre, pour chaque maille, l’équation de l’écoulement. Les calculs sont menés d’une maille à l’autre par approximation successive de manière itérative. Ainsi, à partir des conditions initiales renseignées précédemment, les charges pour chaque maille sont calculées les unes après les autres, plusieurs fois, avec les charges des 4 mailles voisines (itération). Les itérations sont arrêtées lorsqu’une pseudo-stabilisation des charges calculées dans chaque maille est obtenue. Dans notre exemple, la répartition des charges ainsi calculée est obtenue après 300 itérations environ.

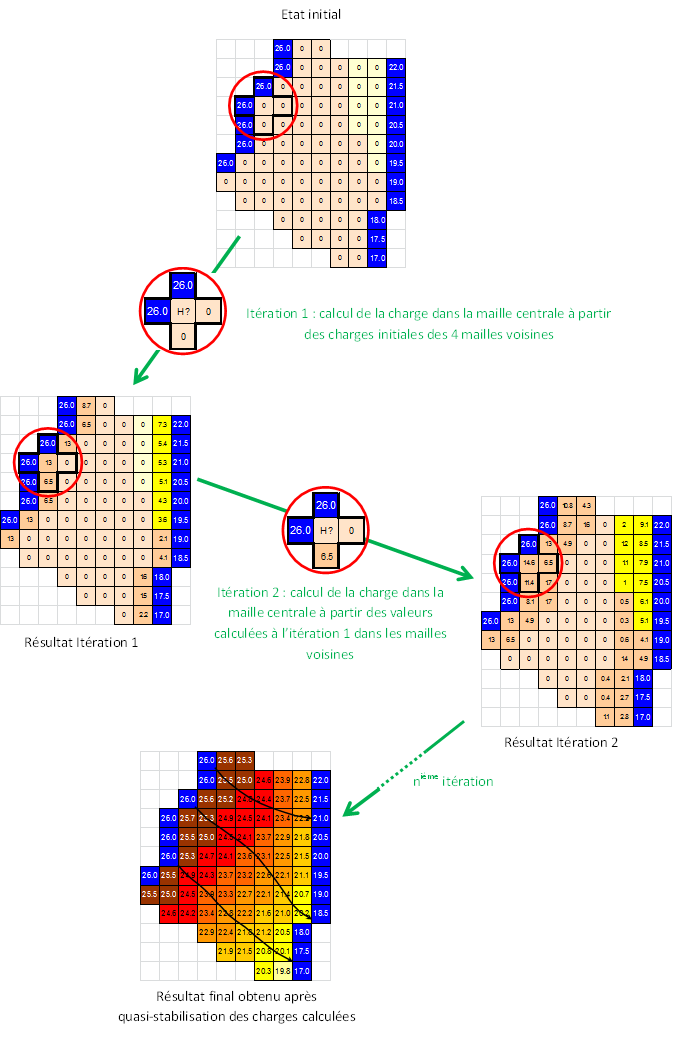
Principe du processus itératif

BRGM

La cohérence des calculs est ensuite vérifiée et le modèle validé, en confrontant les résultats obtenus à des observations faites directement sur le terrain (niveau piézométrique d’un forage , d’une source, d’un cours d’eau).

La simulation d’un pompage est aussi réalisable en modélisation, avec un débit de prélèvement connu.

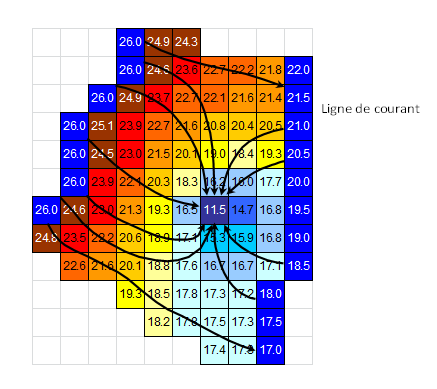
Simulation intégrant un pompage

BRGM

Au final, une étude hydrogéologique à l’aide de l’outil numérique permet de rendre compte du fonctionnement d’un système relativement complexe. Cependant, compte-tenu des différents processus qui entrent en jeu (depuis le choix de la méthode de résolution jusqu’aux hypothèses simplificatrices introduites dans le modèle), une discussion de la pertinence de la modélisation pour le site à étudier est primordiale. De la même manière, la discussion et la critique des résultats obtenus sont obligatoires. En aucun cas, la modélisation ne peut se substituer au jugement humain.

Histoire des modèles SIGES

Des maquettes en plexiglas ou des feuilles de papier calque empilées, dans lesquelles on injecte un courant électrique pour simuler les circulations d’eau souterraine : voilà les premiers modèles d’hydrogéologie ! La rencontre de deux disciplines, la modélisation et l’hydrogéologie, dans les années 1960, va alors permettre une avancée remarquable, aboutissant à la fin de la décennie aux modèles mathématiques modernes. Yves Emsellem [1] et Pierre Pouchan [2], les pionniers de la modélisation en France nous racontent…

Comment a démarré l’histoire des modèles hydrogéologiques ?

Pierre Pouchan : « Dans les années 1960, l’hydrogéologie était une discipline totalement nouvelle. On sortait juste des sourciers ! Sous l’impulsion du Professeur Henri Schœller [enseignant-chercheur au Laboratoire de Géologie de la Faculté des Sciences de Bordeaux], nous avons mis en commun nos connaissances en hydrogéologie et en modélisation, couplées aux connaissances anciennes. Ce travail collaboratif nous a permis de réaliser les premiers modèles « multicouches », représentant les nappes aquitaines. »

Yves Emsellem : « Au début, on ne simulait que les eaux souterraines. La simulation de l’infiltration de l’eau de pluie, du drainage et du débit des rivières était totalement approximative. La rencontre avec les hydrogéologues de Bordeaux a permis de croiser nos connaissances et de passer des modèles analogiques aux premiers modèles mathématiques, beaucoup plus fiables. Nous avons créé le Centre d’Informatique Géologique, où nous a rejoint Ghislain de Marsily [de Marsily G. (1981) - Hydrogéologie quantitative - Masson ed.] qui, plus tard, a fait entrer l’hydrogéologie et sa modélisation à l’Académie des Sciences. »

Pourquoi réaliser des modèles ?

PP : « Avec le concours du BRGM , nous avons établi le premier modèle en 1965 pour les sables inférieurs de l’Eocène moyen, étendu par la suite à l’ensemble des nappes du Bordelais. Le but était de mieux comprendre le fonctionnement des nappes souterraines pour les protéger contre l’invasion par l’eau salée de la Gironde, puis de l’Océan Atlantique ».

YE : « Le Professeur Henri Schœller [Schoeller H. (1962) - Les eaux souterraines - Masson ed.] avait tiré la sonnette d’alarme, à fort juste titre, sur les risques de salure par la Gironde, en cas d’excès d’exploitation des eaux souterraines. Ces risques étaient limités mais réels. Ils devaient être gérés. »

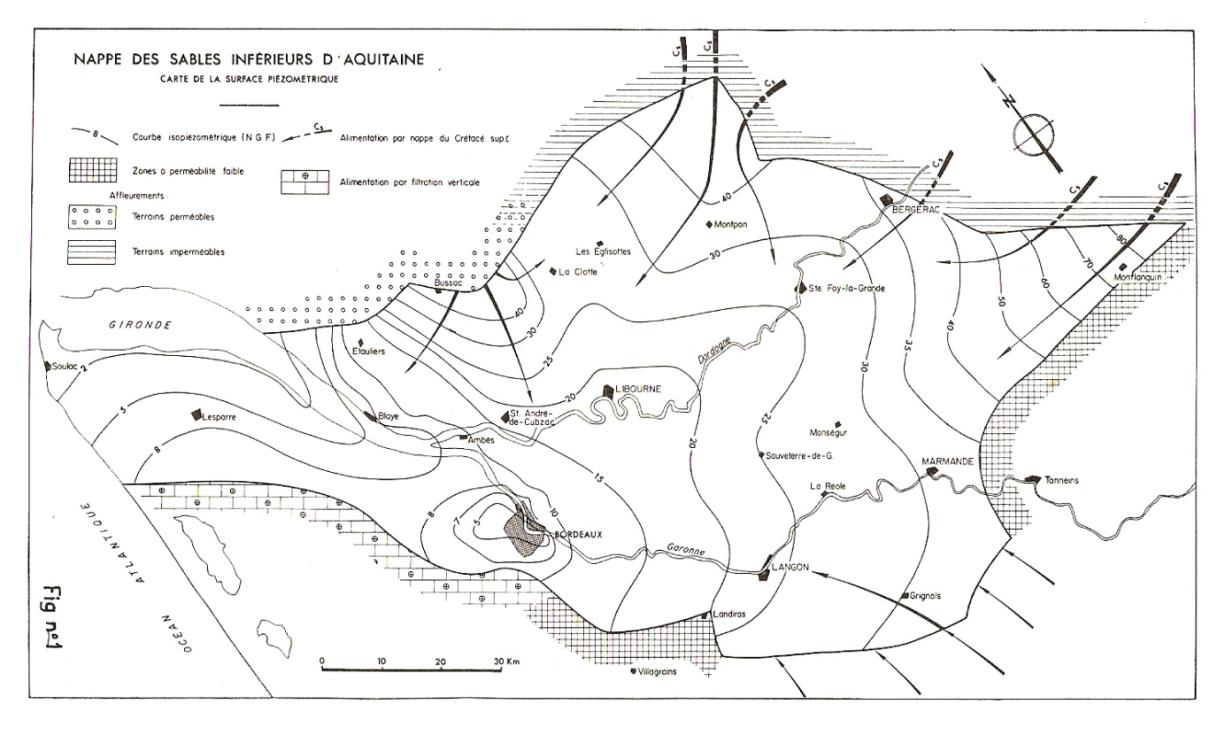
Carte de la surface piézométrique - Nappe des sables inférieurs d’Aquitaine

CESEAU

Les enjeux étaient plutôt importants. Avez-vous rencontré des freins dans la mise en place de ce projet collaboratif ?

YE : « Non, au contraire. Le décret de 1935 imposant une autorisation préalable des forages, gérée par le Service des Mines [service du Ministère de l’industrie, ayant surtout pour mission de résoudre les problèmes liés à l’étude géologique des sols, à l’exploitation du sous-sol et aux travaux souterrains qui en découlent], a été le sésame permettant de regrouper les compétences et de financer les travaux. Nous avons créé les premiers modèles d’Aquitaine de 1965 à 1971, grâce à une symbiose parfaite entre les services techniques de l’Etat (agriculture, équipement…), l’Université de Bordeaux, l’Ecole des Mines [établissement d’enseignement supérieur technique, ayant pour but de former des ingénieurs aptes à diriger les travaux ou recherches dans les exploitations minières], le BRGM , l’Agence de l’Eau et l’ensemble de l’Administration. C’était rarissime à l’époque, quasiment révolutionnaire ! On a réussi à fédérer toutes ces structures et à travailler en bonne intelligence. Par la suite, neuf centres de recherche en France se sont mis à travailler pour passer à la gestion intégrée des ressources en eau souterraine et superficielle, en prenant en exemple le bassin Adour-Garonne. »

Ces premiers modèles analogiques étaient bien loin des modèles numériques que l’on connaît aujourd’hui. A quoi ressemblaient-ils exactement ?

PP : « Nos premiers modèles analogiques, dits rhéoélectriques, étaient des sortes de maquettes, constituées de plaques en plexiglas superposées ou de feuilles en papier calque reliées par des tiges filetées. Chaque feuille représentait une couche du sous-sol. Le découpage de l’espace en blocs élémentaires, les mailles, ont permis de calculer les écoulements et de les comparer aux observations, maille par maille. En fait, il existe une analogie entre le courant circulant dans des feuilles conductrices et la piézométrie des nappes . »

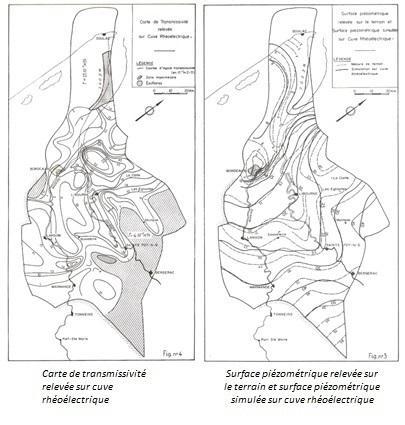
Extrait de la publication n°77. Analogie rhéoélectrique - Etude d’un bassin artésien - Application aux « sables inférieurs d’Aquitaine »

CESEAU

Comment fonctionnaient ces modèles analogiques ?

PP : « Sur le modèle, les zones d’alimentation, d’exutoire et les puits de la nappe étaient figurées par des électrodes, auxquelles étaient appliquées des potentiels électriques, proportionnels aux hauteurs d’eau mesurées sur le terrain. Les potentiels imposés aux puits étaient également proportionnels aux débits soutirés. Ces modèles, dits de régime permanent (indépendants du temps), ne permettaient pas de suivre ou de prévoir l’évolution possible de la nappe qui pouvait être soumise à des prélèvements croissants dans l’avenir proche… voire plus lointain. Pour répondre à ce problème, un nouveau type de modèle, dit de régime transitoire ou non-permanent, a été proposé et réalisé pour la première fois en France, par le Service Géologique d’Alsace et Lorraine. Il s’agissait d’un réseau maillé Résistance-Capacité. L’adjonction d’un condensateur au nœud de chaque maille permettait ainsi d’introduire l’analogie de l' emmagasinement et la notion de temps ! »

YE : « Ces modèles étaient très compliqués ! Leur principal défaut était la complexité des mesures d’intensité en chaque point, puis la transcription en cartes. Ils fonctionnaient, mais à quel prix… L’un d’eux, créé par le Service Géologique d’Alsace et de Lorraine, branché directement par ses partenaires sur une prise de courant, est mort dans un bouquet de très belles étincelles ! Le dernier modèle analogique que j’ai vu a probablement été utilisé jusqu’en 1969 en Union Soviétique, au Centre de cybernétique de Kiev. C’était un modèle à lampes. Il est tombé en panne définitive sous mes yeux, après avoir fonctionné vingt secondes ! »

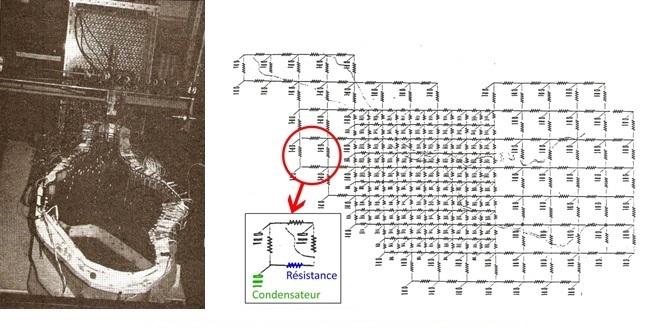
De la cuve rhéoélectrique au système maillé en résistances et capacités

CESEAU

Comment s’est passée la transition vers les modèles numériques ?

PP : « Au début, le modèle numérique ne m’est pas vraiment apparu très performant. Des ordinateurs, considérés comme très puissants, étaient mobilisés pendant des heures sans garantie de succès… Puis est arrivé le microprocesseur, une révolution dans l’informatique. Le modèle numérique a permis, selon Yves Emsellem, la valorisation de l’intellectuel au détriment du manuel ! »

YE : « Nous avons commencé par matérialiser les sept ensembles d’aquifères interconnectés, allant des Sables des Landes au Jurassique. Nous avons alors pu sortir du « monocouche du Tertiaire de Gironde » pour construire le « multicouche d’Aquitaine ». Cette modélisation s’est étendue, au début des années 1970, à l’ensemble de l’Aquitaine et du Poitou-Charentes. La structure du modèle a été reprise, dès 1969-70, pour la planification des ressources et la lutte contre la pollution, puis dans les années 1980-1990 pour l’extension des captages. Très rapidement, les modèles mathématiques numériques ont effacé ces antiquités analogiques ! Le grand intérêt de l’informatique, c’est aussi la pérennité des données et des programmes. »

Modélisations numériques des aquifères, du Plio-Quaternaire au Jurassique, en Aquitaine et Poitou-Charentes

CESEAU

Comment les modèles numériques ont-ils évolué depuis ?

YE : « Techniquement, la grande évolution des modèles a eu lieu dans l’affinage de la physique. L’hydrogéologie, l’agronomie et l’hydrologie, au départ séparées, se sont rassemblées avec l’économie et la démographie, brisant l’hydro-schizophrénie. Avec les progrès sur le non-saturé, les banques de données des Agences de l’Eau et du BRGM (devenue aujourd’hui la BSS), les premiers modèles numériques de terrain… il n’y avait plus de limite ! Le gigantisme a été de pair avec l’étude fine des prélèvements urbains, industriels et agricoles, leurs rejets, les investissements et le développement des Agences de l’Eau. En France, les grands modèles se sont prolongés avec la nappe de la Craie d’Artois-Picardie, puis avec le modèle des ressources en eau de surface et des eaux souterraines, réalisé par Geolab pour l’Agence de l’Eau Seine-Normandie, sur 110 000 km². Dans les années 1970, les modèles se sont développés un peu partout dans le monde. L’UNESCO [Organisation des Nations Unies pour l’éducation, la science et la culture] réalise le grand modèle ERESS des eaux souterraines du Sahara septentrional de l’Algérie et de la Tunisie. Au début des années 2000, l’Observatoire du Sahara et du Sahel lance, à Tunis, un modèle couvrant les pays Algérie-Tunisie-Libye, ou encore, le grand modèle de l’ensemble du Sénégal, de 2000 à 2012, qui reprend d’ailleurs la logique créée dans les années 1960 en Aquitaine !
Aujourd’hui, les modèles sont très gros : celui de l’ aquifère Guarani s’étend au-delà des frontières du Paraguay, de l’Argentine, de l’Uruguay et du Brésil, et dépasse 1,7 millions de km²… »

Propos recueillis par Claire Moras de l’association CESEAU